Les mathématiques jouent un rôle décisif pour comprendre le comportement et le fonctionnement des électrique et systèmes électroniques . Les polynômes, l'algèbre, les probabilités, les intégrations et les différenciations, etc. constituent une partie importante des outils utilisés pour résoudre les systèmes. Avec la complexité croissante des systèmes, des méthodes très sophistiquées sont nécessaires. Les équations différentielles sont largement utilisées pour définir les systèmes de contrôle. Ces équations sont simples à résoudre. Mais la complexité survient lors de la résolution d'équations différentielles d'ordre supérieur. Pour résoudre ces équations différentielles complexes d'ordre supérieur, la méthode mathématique qui s'est avérée efficace est Transformation de Laplace . Comme cette transformation est largement utilisée, il est utile de savoir à quoi elle sert réellement et comment fonctionnent-elles.
Qu'est-ce qu'une transformation de Laplace?
En mathématiques, les transformations sont appliquées pour transformer une variable d'une forme à une autre afin de rendre l'équation facile à gérer. Laplace transforme fait à peu près la même chose. Ils transforment l'équation différentielle d'ordre supérieur en une forme polynomiale, ce qui est beaucoup plus facile que de résoudre directement une équation différentielle.
Mais il existe diverses transformées comme la transformée de Fourier, z transforme ce qui rend la transformation de Laplace spéciale? L'avantage majeur de la transformée de Laplace est qu'elle est définie pour les systèmes stables et instables alors que les transformées de Fourier ne sont définies que pour les systèmes stables.
Formule de transformation de Laplace
Une transformée de Laplace de fonction f (t) dans un domaine temporel, où t est le nombre réel supérieur ou égal à zéro, est donnée par F (s), où il y a  s est le nombre complexe dans le domaine fréquentiel .i.e. s = σ + jω
s est le nombre complexe dans le domaine fréquentiel .i.e. s = σ + jω
L'équation ci-dessus est considérée comme unilatéral Équation de la transformée de Laplace . Lorsque les limites sont étendues à l'ensemble de l'axe réel, le Transformée bilatérale de Laplace peut être défini comme
 Dans des circuits pratiques comme Circuits RC et RL généralement, les conditions initiales sont utilisées, de sorte que les transformées de Laplace unilatérales sont appliquées à des fins d'analyse.
Dans des circuits pratiques comme Circuits RC et RL généralement, les conditions initiales sont utilisées, de sorte que les transformées de Laplace unilatérales sont appliquées à des fins d'analyse.
Comme s = σ + jω, lorsque σ = 0 La transformée de Laplace se comporte comme une transformée de Fourier.

Formules de transformation de Laplace
Conditions d'applicabilité de Laplace Transform
Les transformées de Laplace sont appelées transformées intégrales, il existe donc des conditions nécessaires à la convergence de ces transformées.
 c'est-à-dire que f doit être localement intégrable pour l'intervalle [0, ∞) et selon que σ est positif ou négatif, e ^ (- σt) peut être en décroissance ou en croissance. Pour les transformations de Laplace bilatérales plutôt qu'une valeur unique, l'intégrale converge sur une certaine plage de valeurs connue sous le nom de région de convergence.
c'est-à-dire que f doit être localement intégrable pour l'intervalle [0, ∞) et selon que σ est positif ou négatif, e ^ (- σt) peut être en décroissance ou en croissance. Pour les transformations de Laplace bilatérales plutôt qu'une valeur unique, l'intégrale converge sur une certaine plage de valeurs connue sous le nom de région de convergence.
Propriétés de Laplace Transform:
Linéarité

Linéarité
Changement de temps

Changement de temps
Changement dans le domaine S

Changement dans le domaine S
Inversion du temps

Inversion du temps
Différenciation dans le domaine S

Différenciation dans le domaine S
Convolution dans le temps

Convolution dans le temps
Théorème de la valeur initiale
Le théorème de la valeur initiale est appliqué lorsque dans la transformée de Laplace le degré du numérateur est inférieur au degré du dénominateur  Théorème de la valeur finale:
Théorème de la valeur finale:
Si tous les pôles de sF (s) se trouvent dans la moitié gauche du théorème de valeur finale du plan S est appliqué.
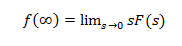 Transformation de Laplace inversée
Transformation de Laplace inversée
En raison de la caractéristique de convergence, les transformées de Laplace ont également une transformée inverse. Les transformations de Laplace présentent un mappage un à un d'un espace fonctionnel à un autre. La formule de la transformée inverse de Laplace est
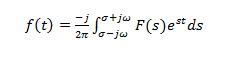 Comment calculer la transformation de Laplace?
Comment calculer la transformation de Laplace?
La transformation de Laplace rend les équations plus simples à gérer. Lorsqu'une équation différentielle d'ordre supérieur est donnée, la transformée de Laplace lui est appliquée, ce qui convertit l'équation en une équation algébrique, la rendant ainsi plus facile à manipuler. Ensuite, nous calculons les racines par simplification de cette équation algébrique. On trouve maintenant une transformée de Laplace inverse d'expression plus simple qui résout l'équation différentielle d'ordre supérieur donnée.

Calcul de la transformation de Laplace
Applications de Laplace Transform
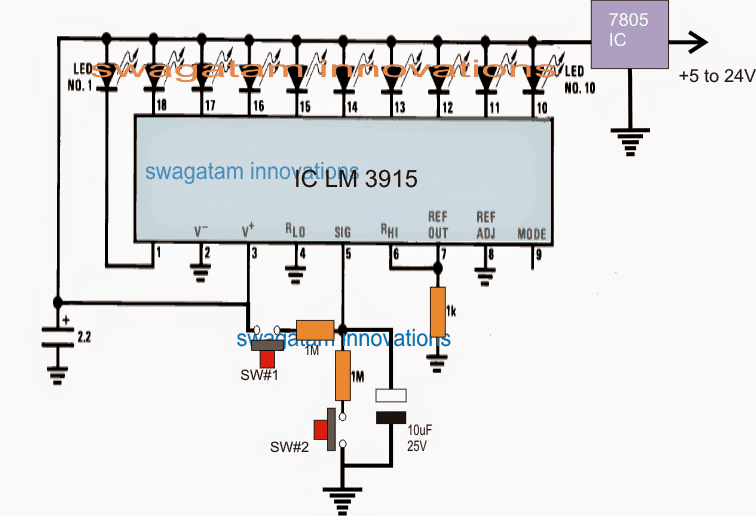
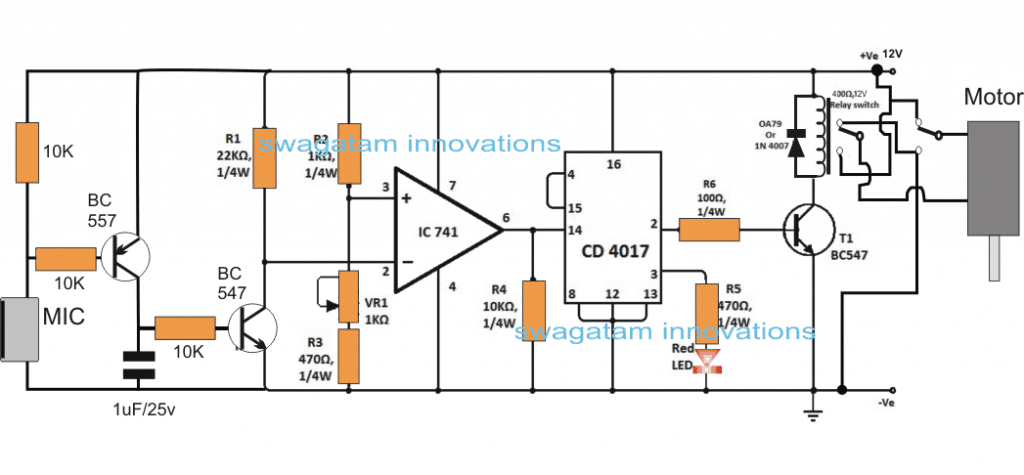
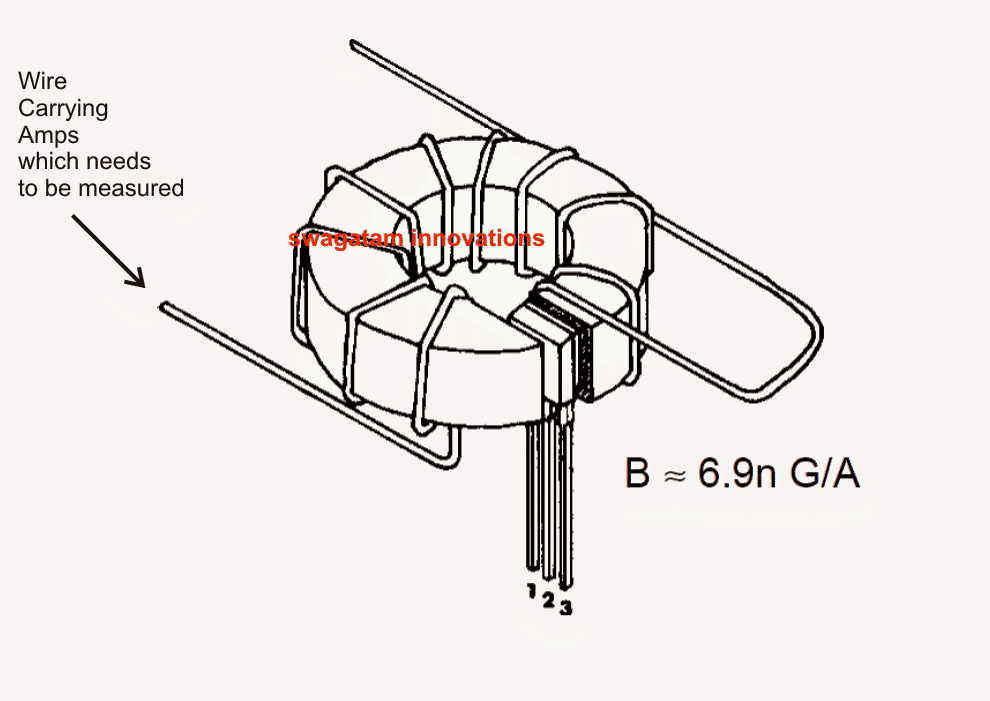
- Analyse de l'électricité et circuits électroniques .
- Décomposer des équations différentielles complexes en formes polynomiales plus simples.
- La transformée de Laplace donne des informations sur les états stables et transitoires.
- Dans l'apprentissage automatique, la transformée de Laplace est utilisée pour faire des prédictions et effectuer des analyses dans l'exploration de données.
- La transformation de Laplace simplifie les calculs dans la modélisation du système.
Application de Laplace Transform dans le traitement du signal
Les transformées de Laplace sont fréquemment choisies pour le traitement du signal. Avec la transformée de Fourier, la transformation de Laplace est utilisé pour étudier les signaux dans le domaine fréquentiel. Lorsqu'il y a de petites fréquences dans le signal dans le domaine fréquentiel, on peut s'attendre à ce que le signal soit lisse dans le domaine temporel. Le filtrage d'un signal est généralement effectué dans le domaine fréquentiel pour lequel Laplace agit comme un outil important pour convertir un signal du domaine temporel au domaine fréquentiel.
Application de Laplace Transform dans les systèmes de contrôle
Les systèmes de contrôle sont généralement conçus pour contrôler le comportement d'autres appareils. Exemple de systèmes de contrôle peut aller d'un simple contrôleur de chauffage domestique à un système de contrôle industriel régule le comportement des machines.
En général, les ingénieurs de contrôle utilisent des équations différentielles pour décrire le comportement de divers blocs fonctionnels en boucle fermée. La transformée de Laplace est utilisée ici pour résoudre ces équations sans perte d'informations variables cruciales.
Caractérisation de systèmes linéaires invariants dans le temps à l'aide de la transformation de Laplace
Pour un système occasionnel ROC associé au système, la fonction est le demi-plan droit. Un système est anti-occasionnel si sa réponse impulsionnelle h (t) = 0 pour t> 0.
Si ROC des fonctions système H (s) inclut l'axe jω alors le L.T.I. le système est appelé un système stable. Si un système occasionnel avec des fonctions système rationnelles H (s) a des parties réelles négatives pour tous ses pôles, alors le système est stable.
La transformée de Laplace est donc un outil crucial dans l'analyse des circuits. On peut dire comme un stéthoscope est au docteur Laplace, les transformations sont à l'ingénieur de contrôle. Comment considérez-vous que Laplace se transforme? De quelle manière vous ont-ils aidé?
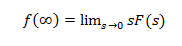 Transformation de Laplace inversée
Transformation de Laplace inversée 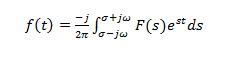 Comment calculer la transformation de Laplace?
Comment calculer la transformation de Laplace?